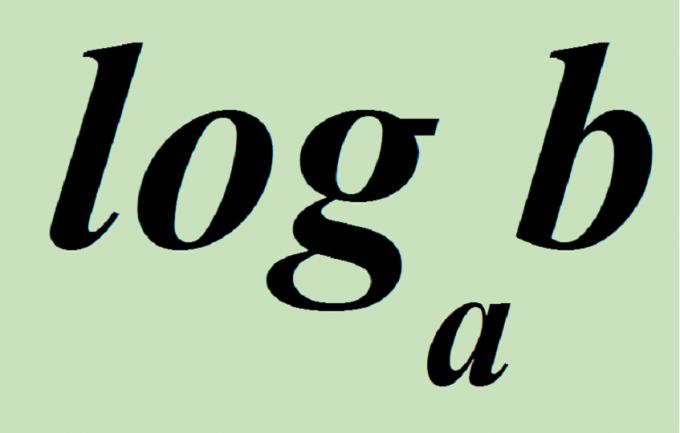Инструкция
1
Из определения логарифма следует, что для того чтобы решить уравнение logaX=b необходимо совершить равносильный переход a^b=x, если a>0 и a не равно 1, то есть 7=logX по основанию 2, то x=2^5, x=32.
2
При решении логарифмических уравнений часто переходят к неравносильному переходу, поэтому необходима проверка полученных корней, путем подстановки в данное уравнение. Например, дано уравнение log(5+2x) по основанию 0,8=1, путем неравносильного перехода, получается log(5+2x) по основанию 0,8=log0,8 по основанию 0,8, можно опустить знак логарифма, тогда получается уравнение 5+2х=0,8, решая данное уравнение получаем х=-2,1. При проверки х=-2,1 5+2х>0, что соответствует свойствам логарифмической функции (область определения логарифмической области положительна), следовательно, х=-2,1 - корень уравнения.
3
Если неизвестное находится в основании логарифма, то подобное уравнение решается теми же способами. Например, дано уравнение, log9 по основанию (x-2)=2. Действуя также как и в предыдущих примерах, получаем (х-2)^2=9, x^2-4x+4=9, x^2-4x-5=0, решая данное уравнение X1=-1, X2=5. Так как основание функции должно быть больше 0 и не равно 1, то остается только корень X2=5.
4
Зачастую при решении логарифмических уравнений необходимо применять свойства логарифмов:
1) logaXY=loda[X]+loda[Y]
logbX/Y=loda[X]-loda[Y]
2) logfX^2n=2nloga[X] (2n - четное число)
logfX^(2n+1)=(2n+1)logaX (2n+1 - нечетное число)
3) logX с основание a^2n=(1/2n)log[a]X
logX с основание a^(2n+1)=(1/2n+1)logaX
4) logaB=1/logbA, b не равен 1
5) logaB=logcB/logcA, c не равен 1
6) a^logaX=X, X>0
7) a^logbC=clogbA
Используя данные свойства, вы можете свести логарифмическое уравнение к более простому типу, а далее решать уже вышеуказанными способами.
1) logaXY=loda[X]+loda[Y]
logbX/Y=loda[X]-loda[Y]
2) logfX^2n=2nloga[X] (2n - четное число)
logfX^(2n+1)=(2n+1)logaX (2n+1 - нечетное число)
3) logX с основание a^2n=(1/2n)log[a]X
logX с основание a^(2n+1)=(1/2n+1)logaX
4) logaB=1/logbA, b не равен 1
5) logaB=logcB/logcA, c не равен 1
6) a^logaX=X, X>0
7) a^logbC=clogbA
Используя данные свойства, вы можете свести логарифмическое уравнение к более простому типу, а далее решать уже вышеуказанными способами.
Видео по теме
Обратите внимание
Логарифм с основанием 10, называется десятичным и обозначается lgX.
Логарифм с основанием 2,7 называется натуральным и обозначается lnX.
Логарифм с основанием 2,7 называется натуральным и обозначается lnX.