Как строить таблицу истинности

Понятие «Таблица истинности» тесно связано с логическими функциями, в этих функциях переменные могут принимать только логические значения – 0 и 1. Логические функции могут быть заданы с помощью таблиц истинности, при этом таблица состоит из аргументов функции и её значений при этих аргументах. При построении таблиц истинности необходимо учитывать порядок выполнения логических операций.

Инструкция

1. Из курса алгебры логик известны основные операции над логическими выражениями, порядок их выполнения следующий:
   1. инверсия;
   2. конъюнкция;
   3. дизъюнкция;
   4. импликация;
   5. эквивалентность.
   Последовательность операций можно менять с помощью скобок.
2. Таблица истинности для сложного выражения строится по следующему алгоритму:
   1. Определяется количество строк по формуле
   количество строк = 2^n + строка для заголовка, где n – количество простых высказываний,
   2. Определяется количество столбцов по формуле
   количество столбцов = количество переменных + количество логических операций,
   3. Строится таблица и заполняется результатами операций в вышеуказанной последовательности, при этом используется таблица истинности простых логических операций.
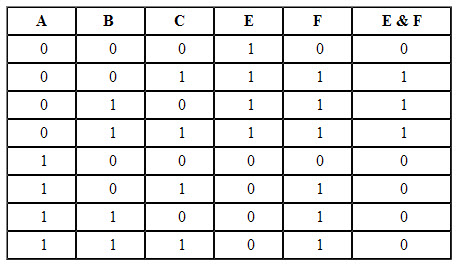
3. К примеру, возьмём такое выражение
   D = ¬ А & (B U C).
   1. В выражении присутствуют высказывания A, B и C, таким образом, n = 3, соответственно
   количество строк = 9
   2. Промежуточные результаты:
   • ¬ А – инверсия, обозначим её буквой E
   • B U C – дизъюнкция, обозначим её буквой F
   • D = ¬ А & (B U C) = E & F – конъюнкция
   3. Таким образом, таблица истинности примет вид, показанный на рисунке.