Инструкция
1
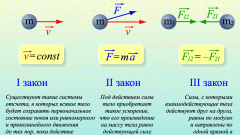
Чтобы определить равнодействующую, нужно найти суммарную силу, действие которой равнозначно совокупному действию всех сил. Для этого применимы законы векторной алгебры, поскольку любая физическая сила имеет направление и модуль. Имеет место принцип суперпозиции, согласно которому каждая сила сообщает телу ускорение независимо от присутствия других сил.
2
Нарисуйте график задачи, используя вектора для представления сил. Начало каждого такого вектора – это точка приложения силы, т.е. само тело или тела, если рассматривается механическая система. Например, вектор силы тяжести должен быть направлен вертикально вниз, направление вектора внешней силы совпадает с направлением движения и т.д.
3
Посмотрите внимательно на график. Определите, как вектора различных сил направлены друг относительно друга. В зависимости от этого произведите расчет их равнодействующей. В соответствии с принципом суперпозиции ее вектор равен геометрической сумме всех сил.
4
Может возникнуть четыре ситуации:Силы направлены в одну сторону. Тогда вектор равнодействующей коллинеарен векторам этих сил и равен их сумме:|F| = |f1| + |f2|.Силы направлены в разные стороны. В этом случае модуль равнодействующей равен разности модулей большей и меньшей силы. Ее вектор направлен в сторону большей силы:|F| = |f1| – |f2|, где |f1| > |f2|.Силы направлены под прямым углом. Тогда вычислите модуль равнодействующей по правилу треугольника сложения векторов. Ее вектор будет направлен по гипотенузе прямоугольного треугольника, образованного векторами сил. При этом начало второго вектора совпадает с концом первого, следовательно, направление равнодействующей снова будет определяться направлением большей силы:|F| = √(|f1|² + |f2|²).Силы направлены под углом, отличным от 90°. По правилу параллелограмма сложения векторов модуль равнодействующей равен:|F| = √(|f1|² + |f2|² – 2•|f1|•|f2|•cos α), где α - угол между векторами сил f1 и f2, направление равнодействующей определяется аналогично предыдущему случаю.
Видео по теме