Вам понадобится
- - карандаш
- - циркуль
- - линейка
Инструкция
1
Чтобы построить произвольный шестиугольник, достаточно нанести на бумагу шесть точек, а затем последовательно соединить их линиями так, чтобы в каждой точке встречались две прямые, которые и являются сторонами фигуры. Некоторые стороны шестиугольника могут даже пересекаться друг с другом.
2
В большинстве случаев по условиям задачи требуется получить равносторонний шестиугольник. Построения подобного рода выполняются следующим образом. Строится окружность, которая затем с помощью циркуля делится на несколько равных частей. Полученные точки последовательно соединяются, в результате получается равносторонний многоугольник.
3
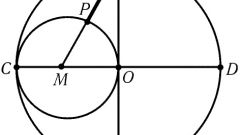
Чертить окружность нужно на основе осевой линии. Начертите произвольную прямую, затем поместите в какую-нибудь ее точку циркуль и с его помощью проведите окружность с радиусом R. Она будет пересекать осевую линию в двух точках, например, 1 и 2.
4
Не меняя раствора циркуля, поместите его в точку 1 и проведите из нее окружность. Таким образом, ее радиус тоже будет равен R. Она пересечет первую окружность в двух точках, обозначьте их как 3 и 4.
5
Теперь установите циркуль в точке 2 и проведите еще одну окружность радиуса R из этой точки. Она тоже пересечет первую окружность в двух местах, которые нужно обозначить как 5 и 6.
6
Последовательно соедините все точки, с 1 по 6. Полученная фигура является равносторонним шестиугольником.
Видео по теме
Обратите внимание
Вместо окружностей можно строить дуги. Этого достаточно, чтобы получать пересечения в требуемых точках, а чертеж не будет загромождаться множеством линий.
Полезный совет
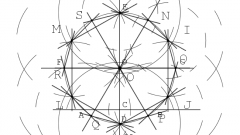
Если остановиться на шаге 4 и соединить точки 1, 3 и 4, можно построить равносторонний треугольник. А если для окружности, в которую вписан шестиугольник, провести вторую осевую линию, перпендикулярную первой, то, построив еще две дополнительные окружности радиусом R из двух новых точек пересечения осевой линии с окружностью, можно получить еще 6 точек. Соединив получившиеся 12 точек, вы получите равносторонний двенадцатиугольник.