Как решать задачу без х

При решении дифференциальных уравнений не всегда явно доступен аргумент x (или время t в задачах физических). Тем не менее – это упрощенный частный случай задания дифференциального уравнения, что часто способствует упрощению поиска его интеграла.

Инструкция

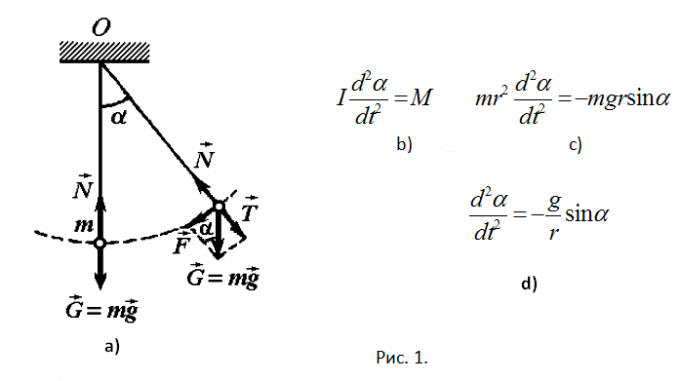
1. Рассмотрите физическую задачу, приводящую к дифференциальному уравнению, в котором отсутствует аргумент t. Это задача о колебаниях математического маятника массой m, подвешенного на нити длиной r, расположенной в вертикальной плоскости. Требуется найти уравнение движения маятника, если в начальный момент маятник был неподвижен и отклонен от состояния равновесия на угол α. Силами сопротивления следует пренебречь (см. рис. 1a).
   
2. Решение. Математический маятник представляет собой материальную точку, подвешенную на невесомой и нерастяжимой нити в точке О. На точку действуют две силы: сила тяжести G=mg и сила натяжения нити N. Обе эти силы лежат в вертикальной плоскости. Поэтому для решения задачи можно применить уравнение вращательного движения точки вокруг горизонтальной оси, проходящей через точку О. Уравнение вращательного движения тела имеет вид, приведенный на рис. 1b. При этом I — момент инерции материальной точки; j — угол поворота нити вместе с точкой, отсчитываемый от вертикальной оси против часовой стрелки; M — момент сил, приложенных к материальной точке.
3. Вычислите эти величины. I=mr^2, M=M(G)+M(N). Но M(N)=0, так как линия действия силы проходит через точку О. M(G)=-mgrsinj. Знак «-» обозначает, что момент силы направлен в сторону противоположную движению. Подставьте момент инерции и момент силы в уравнение движения и получите уравнение, отображенное на рис. 1с. Сокращая массу, возникает соотношение (см. рис. 1d). Здесь нет аргумента t.
4. В общем случае дифференциальное уравнение n-го порядка не имеющее х и разрешенное относительно старшей производной y^(n)=f(y,y’,y’’,...,y^(n-1)). Для второго порядка это y’’=f(y, y’). Решите его подстановкой y’=z=z(y). Так как для сложной функции dz/dx=(dz/dy)(dy/dx), то y’’=z’z. Это приведет к уравнению первого порядка z’z=f(y,z). Решите его любым из известных вам способов и получите z=φ(y, C1). В результате получено dy/dx= φ(y, C1), ∫dy/φ(x,C1)=x+C2. Здесь С1 и С2 — произвольные постоянные.
5. Конкретное решение зависит от вида возникшего дифференциального уравнения первого порядка. Так, если это уравнение с разделяющимися переменными, то оно решается непосредственно. Если это однородное относительно y уравнение, то для решения примените подстановку u(y)=z/y. Для линейного уравнения z=u(y)*v(y).