Инструкция
1
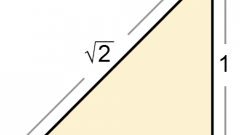
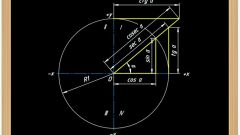
Если рассматриваемый треугольник является прямоугольным, то используйте базовое определение тригонометрической функции синуса для острых углов, который считается как отношение катета, противоположного данному острому углу, к гипотенузе прямоугольного треугольника. Помните следующее - угол, лежащий против гипотенузы, всегда равен 90°. А синус угла в 90° всегда равен единице.
2
Если рассматриваемый треугольник является произвольным, то для того, чтобы найти значение синуса угла а, посчитайте значение косинуса этого угла. Для этого используйте теорему косинусов, согласно которой квадрат длинны одной стороны должен быть равен квадрату длины второй стороны плюс квадрат длины третьей стороны минус удвоенное произведение второй и третьей сторон, умноженное на косинус угла между второй и третьей стороной. Для треугольника KMN KM2=NM2+ NK2-2NM*NK*cosλ. Отсюда посчитайте cosλ=KM2-NM2-NK22NM*NK И по формуле sin2 λ=1-cos2 λ вычислите sinλ=1-cos2λ
3
Еще один способ нахождения синуса угла заключается в использовании двух разных формул площади треугольника. Одна формула - в которой задействованы только длины сторон треугольника (формула Герона). У вас должны быть известны длины всех сторон треугольника. Предположим, стороны равны m, n, k Тогда используйте следующую формулу Герона:S=p△*p△-n*p△-k*(p△)-m) , где полупериметр треугольника: n+k+m2=p△А вторая формула – это произведение длин двух сторон и значения синуса угла между этими сторонами: S (△) = n* k* sinµ.Т.к. значение S одинаково, приравняйте правые части формул:p△*p△-n*p△-k*(p△-m)= n*k* sinµ.И из этой формулы найдите синус угла a, который находится напротив стороны С:sin µ=p△*p△-n*p△-k*(p△-m)n* kСинусы остальных углов можно найти по формулам, аналогичным последней.
Видео по теме