Как найти детерминант

Детерминант (или определитель) матрицы является важнейшей числовой характеристикой квадратной матрицы. Вычисление детерминанта матрицы второго и третьего порядка сводится к применению простейших формул. При нахождении же детерминанта для матриц более высокого порядка потребуются кропотливые вычисления или использование специальных программ или он-лайн сервисов.

Вам понадобится

• - калькулятор;
• - ручка;
• - бумага;
• - компьютер.

Инструкция

1. Чтобы найти детерминант матрицы первого и второго порядка, воспользуйтесь следующими правилами:Для матрицы первого порядка:∆1 = а11,Для матрицы второго порядка:∆2 = а11*а22 – а12*а21, где:∆ - общепринятое обозначение детерминанта,аij – обозначение элемента матрицы, расположенного в i-й строке и в j-м столбце.
2. Чтобы запомнить формулу для вычисления детерминанта матрицы размером 2х2, воспользуйтесь следующей формулировкой:Из произведения элементов, расположенных на главной диагонали (проходящей сверху-вниз, слева-направо), нужно вычесть произведение элементов побочной диагонали (сверху-вниз, справа-налево).
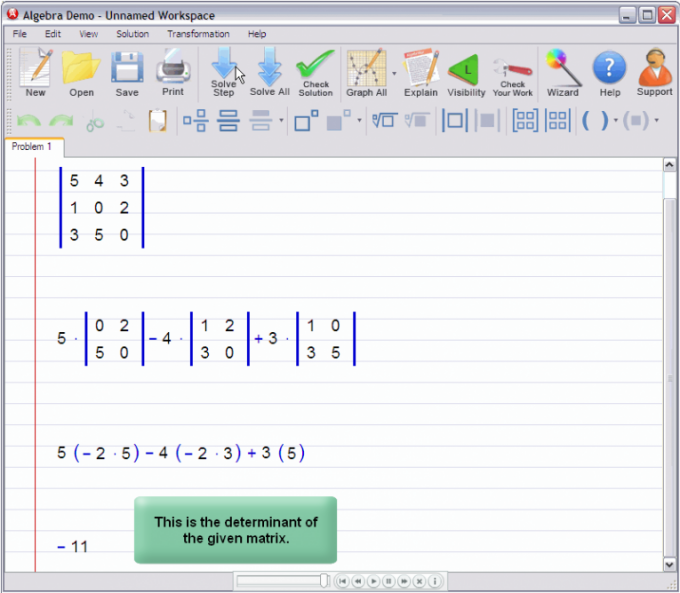
3. Чтобы найти детерминант для матрицы 3х3 выберите в ней произвольную строку или столбец – предпочтительно такой, в котором встречается больше всего нулей. Затем умножьте каждый элемент этой строки (столбца) на детерминант матрицы 2х2, полученной вычеркиванием строки и столбца, содержащих данный элемент. После чего, полученные произведения необходимо сложить. Причем, слагаемые, соответствующие нечетным элементам строки (столбца) нужно брать со знаком плюс, а относящиеся к четным – со знаком минус. Матрица, полученная вычеркиванием i-й строки и j-го столбца, называется дополнительным минором (Mij) к элементу аij основной матрицы.
4. Пример.Если для вычисления детерминанта выбрать первую строку матрицы 3х3, то вышеописанное правило превратится в следующую формулу:∆3 = а11*а22*а33 – а11*а23*а32 – а12*а21*а33 + а12*а23*а31 + а13*а21*а32 – а13*а22*а31
5. Аналогичным образом поступите, если требуется найти детерминант матрицы большей размерности. Только дополнительные миноры для матрицы размерностью, например, 4х4 будут уже иметь размер 3х3, для вычисления детерминанта которых придется выделить миноры меньшего порядка (2х2).
6. Как видно, с увеличением размерности, сложность вычислений детерминанта матрицы растет очень быстро. По научному, количество элементарных вычислений, необходимых для вычисления определителя матрицы n x n обозначается как О(n!) – т.е. сравнимо с числом n! (это даже больше пресловутой геометрической прогрессии). Уже при расчете детерминанта для матрицы 4х4 очень велика вероятность ошибки, поэтому для нахождения детерминантов для "больших" матриц воспользуйтесь он-лайн сервисами и приложениями-калькуляторами.