Автор КакПросто!
Как доказать равенство треугольников
Треугольник является самым простым из типов многоугольников, у которого три угла и три стороны. Стороны образованы отрезками, которые объединены между собой тремя точками на плоскости, образуя при этом жесткую форму. Равенство двух треугольников можно доказать несколькими способами.
Инструкция
Если у
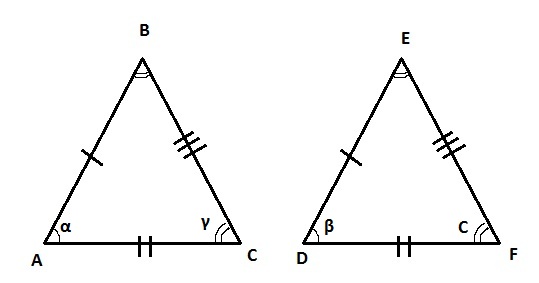
треугольников ABC и DEF две
стороны равны, а угол α, который расположен между двумя
сторонами треугольника ABC,
равен углу β, который расположен между соответствующими сторонами треугольника DEF, то эти два треугольника равны между собой.
Если у треугольников ABC и DEF сторона AB равна стороне DE, а углы, прилегающие к стороне AB, равны углам, прилегающим к стороне DE, то эти треугольники считаются равными.
Если у треугольников ABC стороны AB, BC и CD равны соответствующим им сторонам треугольника DEF, то данные треугольники равны.
Обратите внимание
Если требуется доказать равенство между собой двух прямоугольных треугольников, то это можно сделать при помощи следующих признаков равенства прямоугольных треугольников:
- по одному из катетов и гипотенузе;
- по двум известным катетам;
- по одному из катетов и прилежащему к нему острому углу;
- по гипотенузе и одному из острых углов.
Треугольники бывают остроугольными (если все углы его меньше 90 градусов), тупоугольными (если один из его углов больше 90 градусов), равносторонними и равнобедренными (если две стороны его равны).
Полезный совет
Помимо равенства треугольников между собой, эти же треугольники являются подобными. Подобными треугольниками считаются те, у которых углы равны между собой, а стороны одного треугольника пропорциональны сторонам другого. Стоит отметить, что если два треугольника подобны между собой, то это не гарантирует их равенство. При делении подобных сторон треугольников друг на друга рассчитывается так называемый коэффициент подобия. Также этот коэффициент можно получить путем деления площадей подобных треугольников.
Источники:
- доказать равенство площадей треугольников
