Инструкция
1
Пусть задано множество ребер графа и задано соотношение, по которому можно провести ребро от одной вершины к другой. В качестве примера множество вершин {1, 2, 3, 4, 5, 6, 7, 8}, две вершины x и y состоят в отношении x+y < 8.
2
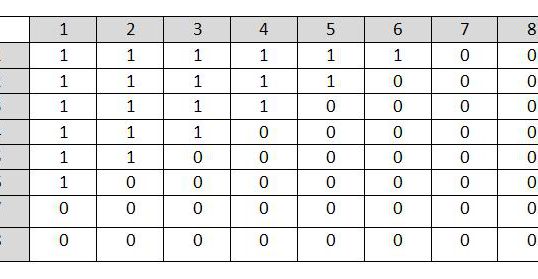
Постройте матрицу смежности вершин. Для этого постройте квадратную таблицу, число строк и столбцов в таблице совпадает с количеством вершин. Затем поставьте 1 на пересечении i-ой строки и j-го столбца, если вершины i и j удовлетворяют заданному соотношению. Поставьте 0 на пересечении i-ой строки и j-го столбца, если соотношение для соответствующих элементов не выполняется.
В нашем примере первая строка заполняется следующим образом:
1+1 < 8, значит на пересечении 1-ой строки и 1-го столбца стоит 1
1+2 < 8, снова 1
1+3 < 8, опять 1
...
1+7 < 8, неверное неравенство, значит этим элементом таблицы будет 0
1+8 < 8, снова 0
3
Чтобы узнать количество ребер, подсчитайте количество единиц в матрице смежности, при этом следует не задваивать ребра.
В примере получилась симметричная матрица, поэтому подсчитали сначала единицы выше главной диагонали матрицы (отмечены голубым), а затем и единицы на главной диагонали (отмечены красным). Общее количество ребер получилось 12.
4
Постройте матрицу инциденций (ребер). Для этого начертите таблицу, число строк в ней равно числу вершин графа, а число столбцов - количеству ребер. Проставьте единицы в тех строках, которые будут соединены ребром. Ребра, ведущие от вершины к ней же, называют петлями и добавляют в конец матрицы. В столбцах, соответствующих петлям, стоит только одна единица в отличие от остальных ребер.
5
Теперь начертите граф. Разместите вершины на бумаге произвольным образом и соедините их ребрами, используя построенные таблицы. Вершины, не соединенные ребрами, называются изолированными.