Вам понадобится
  • - ручка;
  • - бумага для записей;
  • - калькулятор.
Инструкция
1
Прямая на плоскости описывается уравнением: ax+bу+с = 0, где х,y – координаты по оси 0х и оси 0у какой-либо точки прямой; a, b, с – числовые коэффициенты. Причем a и b не могут равняться нулю одновременно. Такой вид записи называется общим уравнением прямой.
2
Также прямую можно задать выражением вида: y = kx+c. Это уравнение прямой с угловым коэффициентом k, который является тангенсом угла, образующегося при пересечении данной прямой с осью 0х.
3
Зная координаты двух точек А (х1;y1), В (х2;у2), вы можете записать уравнение прямой, проведенной через эти точки, используя пропорцию: (у-у1)/(у1-у2)=(х-х1)/(у1-у2). Далее, преобразовав это равенство, приведите его к виду как в шаге 1 или 2.
4
Рассмотрите алгоритм решения задачи на конкретном примере. Даны три вершины треугольника с известными координатами: А (9;8), В (7;-6), С (-7;4). Напишите уравнение прямых, образующих его.
5
Найдите уравнение для прямой АВ. Примените формулу из шага 3, подставив значения координат точек А и В: (у-8)/(8-(-6)) = (х-9)/(9-7). Преобразуйте его: (у-8)/14 = (х-9)/2 или 2(у-8) = 14(х-9). Сократите уравнение, разделив левую и правую части на два, и раскройте скобки: у = 7х-63+8 = 7х-55.
Уравнение для АВ: у = 7х-55. Или: 7х-у-55 = 0 (АВ).
6
Аналогично напишите уравнение для прямой ВС: (у-(-6))/(-6-4) = (х-7)/7-(-7)). (у+6)/(-10) = (х-7)/14. 7(у+6) = -5(х-7). 7у+42 = -5х+35. 7у = -5х-7. у = -5/7х-1.
Уравнение для ВС: y = -5/7х-1. Или: -5х-7у-7 = 0 (ВС).
7
Затем уравнение для прямой СА: (у-8)/(8-4) = (х-9)/(9-(-7)). 16(у-8) = 4(х-9). 4у-32 = х-9. 4у = х-9+32. у = 0,25х+5,75.
Уравнение для СА: у = 0,25х+5,75. Или: х-4у+23 = 0 (СА).
8
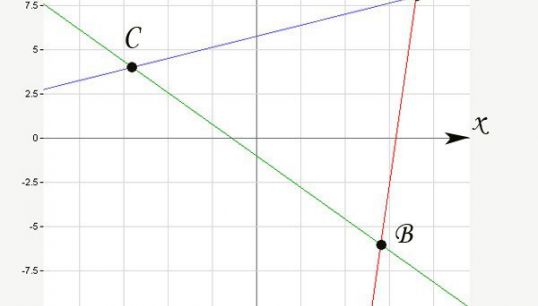
Вы составили уравнения трех сторон фигуры. Для самопроверки постройте треугольника в системе координат. Найдите на чертеже значения пересечений прямых с осью 0у. Сравните эти координаты с полученными в уравнении. Например, для (BC) при y = 0, х = -1,4.