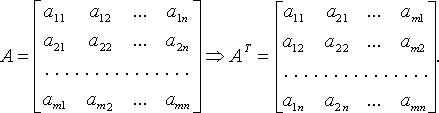Как транспонировать матрицу

По определению из курса линейной алгебры матрицей называется совокупность чисел расположенных в виде таблицы с количеством строк m и количеством столбцов n. Элементами матрицы могут быть, например комплексные или действительные числа. Матрицы обозначаются записью вида A = (aij), где aij – элемент, расположенный на i – й строке и j – ом столбце.

Инструкция

1. Пусть дана некоторая матрица A = (aij) размерности m*n.
   Матрица, полученная из матрицы A путём перестановки строк и столбцов, называется транспонированной матрицей и обозначается AT. Элементы матрицы AT составляются из элементов матрицы A следующим способом
   aij = aji, i = 1,…,m; j = 1,…,n
   Матрица AT = (aij), при этом имеет размерность n*m.
   Квадратная матрица называется симметричной, если для неё верно равенство A = AT.
2. Для транспонированных матриц верны следующие соотношения:
   (AT)T = A,
   (A + B)T = AT + BT,
   (A * B)T = AT * BT,
   (? * A)T = ? * AT, где ? – скаляр,
   det A = det AT, т.е определитель матрицы равен определителю транспонированной матрицы.