Автор КакПросто!
Как найти высоты треугольника
Геометрия - не только школьный предмет, по которому надо получить хорошую оценку. Расчет высоты треугольника может понадобиться и в практической жизни. Например, если вы строите дом с высокой крышей и вам надо рассчитать количество и толщину бревен.
Вам понадобится
- Линейка Угольник Карандаш Транспортир Таблицы синусов и косинусов
Инструкция
Постройте треугольник с заданными параметрами. Вам известны либо два угла треугольника и сторона между ними, либо угол и длина двух сторон, между которыми он
находится, либо три
стороны.
Обозначьте вершины углов треугольника как А, В и С. Обозначьте углы соответственно как ?,?, ? Противолежащие стороны
обозначьте как a,b,c.
Вспомните,
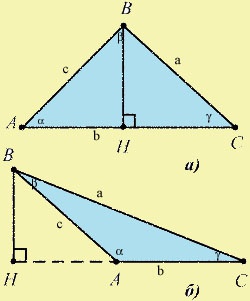
что такое высота. Это перпендикуляр, проведенный из угла треугольника к его противоположной стороне. Возьмите угольник и проведите такие перпендикуляры ко всем сторонам треугольника. Обозначьте высоты буквой h с соответствующими сторонам треугольника индексами a,b,c.
Вычислите длину всех сторон треугольника и все его углы по теоремам синусов и косинусов.
Вычислите высоту, опущенную из заданного угла, по формуле: высота, опущенная из угла С, равна произведению синуса любого другого угла на длину прилежащей к нему стороны.
Видео по теме

Обратите внимание
Высоты остроугольного треугольника находятся внутри него. У тупоугольного треугольника одна высота (та, которая идет от тупого угла) проходит внутри треугольника, а две другие - вне его. У прямоугольного треугольника две высоты совпадают с катетами, а одна находится внутри треугольника. Все три высоты пересекаются в ортоцентре, который может находиться внутри, вне или на катете треугольника. В прямоугольном треугольнике две высоты известны, поскольку они же являются катетами. Третью высоту находим по теореме Пифагора,отняв от квадрата отрезка АС, который является одновременно гипотенузой треугольника СDА, квадрат отрезка АD. Размер этого отрезка легко вычислить, зная о подобии треугольников. Гипотенуза АВ относится к гипотенузе СВ так же, как катет ВС относится к катету DB. Стороны прямоугольного треугольника вычисляются по теореме Пифагора. Стороны остроугольного треугольника вычисляются по теоремам синуса или косинуса
Полезный совет
Для определения синусов и косинусов пользуйтесь математическими таблицами.

