Как найти угол между прямой и плоскостью, если даны точки

Задача относится к аналитической геометрии. Ее решение можно найти на основе уравнений прямой и плоскости в пространстве. Таких решений, как правило, несколько. Все зависит от исходных данных. При этом любой вид решения без больших трудозатрат может быть переведен в другой.

Инструкция

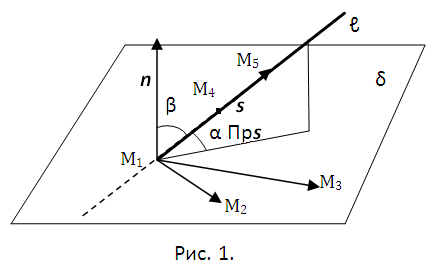
1. Поставленную задачу наглядно иллюстрирует рисунок 1. Вычислению подлежит угол α между прямой ℓ (точнее, ее направляющим вектором s) и проекцией направления прямой на плоскость δ. Это неудобно тем, что тогда приходится искать направление Прs. Гораздо проще сначала найти угол β между направляющим вектором прямой s вектором нормали к плоскости n. Очевидно (см. рис. 1), что α=π/2-β.
2. Фактически для решения задачи осталось определить нормальный и направляющий векторы. В поставленном вопросе упомянуты заданные точки. Только не указано - какие именно. Если это точки, определяющие как плоскость, так и прямую, то их не мене пяти. Дело в том, что для однозначного задания плоскости требуется знать три ее точки. Прямая однозначно задается двумя точками. Потому следует считать, что даны точки М1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3) (задают плоскость), а также M4(x4,y4,z4) и M5(x5,y5,z5) (задают прямую).
3. Для определения направляющего вектора s вектора прямой совсем не обязательно располагать ее уравнением. Достаточно положить s=M4M5, и тогда его координаты s={x5-x4, y5-y4, z5-z4} (рис. 1). Это же можно сказать и о векторе нормали к поверхности n. Для его вычисления найдите векторы М1М2 и М1М3, показанные на рисунке. M1M2={x2-x1, y2-y1, z2-z1}, M1M3={x3-x1, y3-y1, z3-z1}. Эти векторы лежат в плоскости δ. Нормаль n перпендикулярна плоскости. Поэтому положите ее равной векторному произведению М1М2×М1М3. При этом совершенно не страшно, если нормаль окажется направленной противоположно той, которая приведена на рис. 1.
4. Векторное произведение удобно вычислять с использованием вектора-определителя, который следует раскрывать по первой его строке (см. рис. 2a). Подставьте в представленный определитель вместо координат вектора а координаты М1М2, вместо b – M1M3 и обозначите их А, B, C (именно так записываются коэффициенты общего уравнения плоскости). Тогда n={А,B,C}. Для определения угла β используйте скалярное произведение (n,s) и способ его вычисления в координатной форме. сosβ=(A(x5-x4)+B(y5-y4)+C(z5-z4))/(|n||s|). Так как для искомого угла α=π/2-β (рис. 1), то sinα=cosβ. Окончательный ответ приведен на рис. 2b.